1- Scrieţi un program în care să se efectueze principalele operaţii cu o listă simplu înlănţuită (inserare, căutare, ştergere) alocarea elementelor făcându-se printr-un alocator propriu de memorie.

1- Se consideră o masă circulară la care sunt aşezaţi copii şi fie n un număr întreg pozitiv. Pornind de la un anumit copil ei încep să numere pe rând. Atunci când unul din copii ajunge numărul n acesta se ridică de la masă şi se reia numărătoarea pornind de la 1. Jocul se opreşte atunci când râmâne un singur copil.

Realizaţi un program ce utilizează o listă circulară pentru a afişa ordinea în care copiii se ridică de la masă.

1- Să scrie un program care să calculeze produsul a două polinoame utilizându-se pentru reprezentarea unui polinom o listă simplu înlănţuită.

1- Se citesc de la tastatura mai multe cuvinte. Să se determine frecvenţa de apariţie a cuvintelor în textul respectiv utilizându-se o tabelă de dispersie.

1- Să se implementeze o listă dublu înlănţuită ale cărei elemente să fie studenţii unei facultăţi.

Programul va conţine funcţii pentru:

• crearea listei vide
• afişarea elementelor listei
• căutarea unui student în listă
• adăugarea unui student la lista (la început, la sfârşit, după un anumit nod specificat).
• ştergerea unui anumit student din listă.

1- Într-o localitate de frontieră se găsesc un număr n de puncte vamale. Fiecare maşină ce doreşte să treacă graniţa trebuie să treacă printr-un astfel de punct. Traficul fiind foarte intens, la fiecare dintre puncte se formează câte o coadă. O maşină ce vine se aşează la una dintre acestea (la cea mai mică).

Să se se realizeze un program care va simula traficul în vamă.

1- Să se realizeze un program care calculează forma poloneză a unei expresii aritmetice.

2- Să se scrie un program pentru parcurgerea DFS (Depth First Search) a unui graf conex neorientat.

Exemplu:

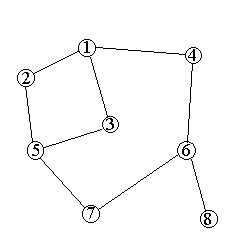
Pentru graful

parcurgerea DFS va afişa vârfurile în ordinea: 1, 2, 5, 3, 7, 6, 4, 8.

2- Să se scrie un program pentru parcurgerea BFS (Breadth First Search) a unui graf conex neorientat.

Exemplu:

Pentru graful anterior parcurgerea BFS este: 1, 2, 3, 4, 5, 6, 7, 8.

2- Să se scrie un program pentru parcurgerea D a unui graf conex neorientat.

Pentru graful anterior ordinea de vizitare a nodurilor este: 1, 2, 3, 4, 6, 7, 8, 5.

2- Scrieţi un program care testează dacă un graf neorientat este conex.

2- Scrieţi un program care pentru un graf neorientat determină toate componentele conexe.

2- Fie un graf neorientat G=(V, E). Scrieţi un program care să verifice dacă graful dat este aciclic.

2- Un graf neorientat G=(V, E) este eulerian dacă şi numai dacă este conex şi gradul fiecărui vârf este par. Scrieţi un program care pentru un graf dat verifică dacă este eulerian, iar în caz de răspuns afirmativ determină un ciclu eulerian.

2- Fie un graf neorientat G=(V, E). Realizaţi un program care să determine toate ciclurile hamiltoniene ale lui G.

2- Fie un graf neorientat G=(V, E). Se defineşte distanţa dintre două noduri u şi v ca fiind numărul de muchii de pe drumul cel mai scurt ce uneşte pe u cu v. Scrieţi un program care să determine distanţa minimă între două noduri specificate.

2- Fie un graf neorientat G=(V, E). Se defineşte muchie critică acea muchie care prin eliminarea ei conduce la mărirea numărului de componente conexe ale grafului. Scrieţi un program care să determine toate muchiile critice ale unui graf dat.

2- Fie G=(V, E) un graf orientat unde V={1, 2,..., n} este mulţimea nodurilor şi E este mulţimea arcelor (). Pentru reprezentarea grafului se utilizează matricea costurilor C:

Fie i₀ un vârf al grafului. Să se determine pentru toate vârfurile , dacă există, un drum de cost minim de la i₀ la j.

2- (Arborele partial de cost minim) Fie G=(V, E) un graf neorientat unde V={1, 2,..., n} este mulţimea nodurilor şi E este mulţimea muchiilor (). Pentru reprezentarea grafului se utilizează matricea costurilor C:

Să se determine un graf parţial G₁=(V, E₁) cu proprietatea că suma costurilor tuturor muchiilor este minimă. Graful parţial de cost minim este chiar un arbore.

2- Fie G=(V, E) un graf orientat unde V={1, 2,..., n} este mulţimea nodurilor şi E este mulţimea arcelor (). Graful orientat G se numeşte tare conex dacă pentru orice pereche de vârfuri , există un drum de la u la v şi un drum de la de la v la u.

Se poate arăta că relaţia de tare conexitate este o relaţie de echivalenţă. În cazul în care un graf orientat nu este puternic conex atunci el se poate descompune în mai multe componente puternic conexe. O astfel de componentă este determinată de un subgraf al grafului iniţial.

2- Se consideră procesul de proiectare a unei plăci electronice cu N componente electronice (1<=N<=100). Pentru fiecare componentă I se cunoaşte numărul de interconexiuni. Se consideră graful determinat de mulţimea pinilor şi mulţimea interconectărilor posibile ale tuturor componentelor, precum şi lungimile lor. Dintre toate modalităţile de interconectare posibile se cere cea corespunzătoare arborelui de acoperire minimă.

Intrarea se compune din mai multe plăci electronice. Descrierea unei plăci conţine pe prima linie numărul N de componente şi numărul M de interconexiuni. Dacă N=0 atunci procesul de introducere date se încheie. O interconexiune se caracterizează prin trei valori: două vârfuri v₁ şi v₂ precum şi lungimea acesteia l.

Ieşirea programului va consta dintr-o linie de text pentru fiecare set de date de test. Ea va conţine numărul testului (se începe numerotarea cu 1), precum şi costul interconectării de lungime minimă.

Exemplu

Intrare

5 7

1 2 40 2 3 35 1 5 27 1 4 37 4 5 30 2 4 58 3 4 60

0 0

Iesire

Cazul 1: [1 5] [4 5] [2 3] [1 2]

Interconectarea de cost minim are valoarea 132

2- Pentru asigurarea securităţii activităţii dintr-un combinat chimic s-a apelat la o companie de pompieri. Instalarea companiei presupune stabilirea locurilor de instalare a comandamentului şi a posturilor de supraveghere. Pentru aceasta sunt disponibile în cadrul combinatului n puncte de control. Pentru fiecare pereche de puncte de control se cunoaşte dacă există o legătură directă între ele şi în caz afirmativ distanţa dintre ele. Se cunoaşte de asemenea că între oricare două puncte de control există un drum direct sau indirect. Odată stabilite amplasamentele comandamentului şi a punctelor de supraveghere în câte unul dintre cele n puncte de control este posibil să se ajungă de la comandament la fiecare punct de supraveghere parcurgând un anumit drum. Evident, este de dorit ca lungimea acestui drum să fie minimă şi maximul dintre lungimile drumurilor minime pentru fiecare punct de supraveghere în parte să fie cât mai mic posibil. Se cere determinarea punctului de control în care trebuie instalat comandamentul cât şi drumurile care vor fi parcurse de la comandament la fiecare punct de supraveghere astfel încât aceste drumuri să aibă lungimi minime şi cel mai lung dintre ele să fie cât mai scurt posibil.

Intrarea constă din mai multe date de test. Descrierea unei zone începe pe prima linie cu două numere naturale n şi m corespunzând numărului de puncte de control (1<=n<=100) respectiv numărului de perechi de puncte de control ce sunt direct conectate (1<=m<=10000). În continuare se citesc m perechi de puncte de control. Intrarea se termină atunci când n=0.

Ieşirea programului va consta dintr-o linie de text pentru fiecare set de date. Ea va conţine numărul testului (se începe numerotarea cu 1), precum şi numărul punctului de control unde se va instala comandamentul.

Exemplu :

Intrare

Iesire

Cazul 1: Comandamentul in 3

Drumul pina la 1: 3 6 7 8 1

Drumul pina la 2: 3 6 7 8 1 2

Drumul pina la 4: 3 4

Drumul pina la 5: 3 4 5

Drumul pina la 6: 3 6

Drumul pina la 7: 3 6 7

Drumul pina la 8: 3 6 7 8

Drumul pina la 9: 3 9

2- Fie G=(V, E) un graf orientat unde V={1, 2,..., n} este mulţimea nodurilor şi E este mulţimea arcelor (). Fiecărui arc din E i se asociază o valoare pozitivă c_ij numită lungimea arcului. Să se calculeze drumurile de lungime minimă pentru oricare perechi de noduri i, j. (Pentru această problemă vom aplica metoda programării dinamice.)

2- Fie G(V, E) un graf orientat unde V={1, 2,..., n} este mulţimea nodurilor şi E este mulţimea arcelor (). Pentru reprezentarea grafului se utilizează matricea costurilor C:

Să se determine un circuit care să treacă exact o dată prin fiecare vârf şi care să aibă cost minim (circuit hamiltonian).

2- Se cunoaşte harta unui oraş dată prin străzi şi intersecţii. Într-o intersecţie pot sosi mai multe străzi. Unele străzi sunt cu sens unic, altele au dublu sens de circulaţie. Un automobilist pleacă dintr-o intersecţie şi vrea să ajungă printr-un parcurs minim la o altă intersecţie. Scrieţi un program care pentru o hartă dată determină lungimea drumului minim între mai multe perechi de intersecţii.

Intrarea va fi formată dintr-o hartă. Pe prima linie se citeşte un număr natural n (1<=n<=100). Pe fiecare din următoarele n linii vom avea mai multe perechi de numere (v,l) ce reprezintă faptul că distanţa dintre intersecţia i (corespunzatoare liniei) şi intersecţia v este l. Datele de pe o linie se termină printr-o pereche 0 0. După aceea urmează mai multe perechi de intersecţii între care se va determina distanţa minimă precum şi traseul de urmat.

Ieşirea va fi formată din mai multe linii, fiecare corespunzând unei perechi de intersecţii.

Exemplu

Intrare

5

2 6 4 7 0 0

3 5 4 8 5 4 0 0

2 2 0 0

3 3 5 9 0 0

1 2 3 7 0 0

1 5 3 1 0 0

Iesire

Cazul 1: distanta de la 1 la 5 este 10 prin intersectiile 2

Cazul 2: distanta de la 3 la 1 este 8 prin intersectiile 2 5

3. Arbori

3- Să se parcurgă un arbore binar în preordine.

Exemplu:

Pentru arborele

parcurgerea în preordine ne conduce la 1,2, 3,4,5,6,7,8,9.

3- Să se parcurgă un arbore binar în inordine.

3- Se consideră dată o expresie logică formată din n variabile logice reprezentate de o singură literă şi operatorii & (AND), | (OR), ! (NOT) (nu avem paranteze). Expresia este reprezentată sub forma unui arbore binar. Se cere să se scrie programul care crează structura de date corespunzătoare unei expresii logice date şi cercetează existenţa unei combinaţii de valori logice, pentru care expresia dată prin arborele binar ia valoarea logică TRUE.

Intrarea este formată din mai multe expresii logice. O expresie este dată pe câte o linie şi are maxim 80 de caractere. Expresia && indică sfirşitul datelor de intrare.

Ieşirea programului va consta dintr-o linie de text pentru fiecare set de date de test. Ea va conţine numărul testului (se începe numerotarea cu 1), precum şi o combinaţie de valori logice care fac expresia adevărată fie 'Nu avem solutie' în caz că nu există.

Exemplu

Intrare

Ieşire

Cazul 1: Solutie a=0 b=0 c=0 d=0

Cazul 2: Nu avem solutie!

3- Să se contorizeze frecvenţa de apariţie a tuturor cuvintelor citite de la tastatură. Separatorii sunt: spaţiu, tab şi newline.

3- Scrieţi un program care să creeze un arbore binar de sortare, să-l parcurgă în inordine şi să permită inserarea şi ştergerea unui nod specificat.

3- Informaţiile pentru medicamentele unei farmacii se referă la numele medicamentului, preţul lui, cantitatea, data primirii şi data expirării. Evidenţa medicamentelor se ţine cu un program care are drept structură de date un arbore. Să se scrie un program ce crează această structură de date, tipăreşte medicamentele în ordine lexicografică şi elimină apoi medicamentele care au data de expirare peste o dată specificată.

Intrarea este formată din mai multe linii. Pe fiecare linie avem câte un medicament dat sub forma:

[nume_produs] [pret] [cantitate] [zi] [luna] [an].

Introducerea medicamentelor se termină cu o linie pe care avem doar '&'. Urmează apoi o dată calendaristică după care vor fi eliminate medicamentele ce au data de exprirare după.

Ieşirea este formată prin afişarea medicamentelor rămase, în ordine lexicografică.

Exemplu

Intrare:

aspirina 500 20 2 10 2000

Ieşire:

aspirina captopril nifedipin

3- Un heap este un arbore binar complet (frunzele lipsă se află pe ultimul nivel, în partea dreaptă) iar valoarea unui nod părinte nu este mai mare decât valorile descendenţilor săi (vezi ultima problemă de la sortări).

1. Scrieţi o funcţie care şterge elementul minimal din heap.

3- Se citeste de la intrare un arbore binar dat în reprezentarea STANG-DREPT:

c) Să se transforme arborele dat prin reprezentarea lui într-un heap şi să se afişeze vectorul rezultat.

Exemplu: Se consideră arborele:

3- Se citeşte de la intrare un şir de valori numerice întregi, pe o linie, separate de spaţii, şir care se încheie cu o valoare 0. Să se memoreze aceste valori într-un vector.

Considerând că vectorul dat este reprezentarea implicită a unui arbore binar:

a) Să se afişeze în preordine conţinutul arborelui.

b) Să se determine dacă arborele este heap.

c) Dacă arborele introdus este heap, să se afişeze elementele în ordine descrescătoare prin extrageri succesive din heap.

Exemplu:

3- Să se parcurgă un arbore oarecare în A-preordine şi A-postordine.

4. Metoda Greedy

4- Fie o mulţime de intervale

,

unde . Să se determine mulţimea maximală de intervale disjuncte două câte două.

4- (Problema rucsacului) O persoană are un rucsac cu care poate transporta o greutate maxima GT. Persoana are la dispozitie n obiecte şi cunoaşte pentru fiecare obiect greutatea precum şi câştigul care se obţine în urma transportului său la destinaţie. Se cere să se precizeze ce obiecte trebuie să transporte persoana astfel încât câştigul să fie maxim.

4- Se dau n numere întregi nenule b₁, b₂, ..., b_n şi m numere întregi nenule a₁, a₂, ...,a_m. Să se determine o submulţime a mulţimii B={b₁,..,b_n} care să maximizeze valoarea expresiei

ştiind că şi că .

Indicaţie:

- Sortăm elementele celor două mulţimi A şi B.

- Dacă elementele mulţimii A sunt numere întregi pozitive alegem ultimele m elemente din şirul ordonat B.

- Dacă elementele mulţimii A sunt negative alegem primele m elemente ale şirului B.

- Dacă mulţimea A are k elemente negative şi p elemente pozitive (m=k+p) vom alege primele k elemente ale şirului B precum şi ultimele p elemente ale şirului B.

4- O agentie de turism are de efectuat un număr de n curse săptămânale. Pentru fiecare cursă se ştie data plecării şi data sosirii (acestea sunt date in ore relativ fata de ora 0 a primei zile a săptămânii). Să se determine numărul mimim de autocare necesar pentru a se asigura efectuarea tuturor curselor. Un autocar nu poate efectua într-o perioadă de timp decât o singură cursă.

4- Problema comis-voiajorului. Se dă un graf neorientat G complet. Să se determine un ciclu hamiltonian de lungime minimă.

4- Se dau şirurile S₁, S₂,..., S_m ordonate crescător fiecare având lungimile L₁, L₂,..., L_m. Se cere să se interclaseze cele m şiruri cu un număr minim de operaţii. Se ştie că la interclasarea a două şiruri, numărul de operaţii este egal cu suma elementelor celor două şiruri care se interclaseaza.

4- O întreprindere primeşte la un moment dat t=0 spre execuţie n lucrări. Fiecare lucrare necesită acelaşi timp de execuţie =1. Pentru executarea lucrării a i-a, i=1,..,n unitatea respectivă are un beneficiu C_i numai dacă lucrarea a fost executată cu respectarea termenului final de livrare T_i. Întreprinderea nu poate executa două lucrări în acelaşi timp. Se cere să se determine numărul de lucrări ce îl poate executa întreprinderea astfel încât beneficiul să fie maxim.

4- Fie S o sumă de bani. Să se exprime această sumă de ani într-un număr minim de monede de 25,10,5 şi 1 unităti.

4- Se consideră o reţea pătratică, care conţine segmente ale căror extremităţi sunt puncte adiacente situate pe aceeaşi linie sau aceeaşi coloană.

Se cere să se scrie un program care să numere câte pătrate pot fi identificate în reţeaua dată (indicând şi lungimea laturii). Opţional, se cere reprezentarea grafică.

4- O staţie de spălare a maşinilor trebuie să spele n autovehicule. Se cunoaşte timpul t_i în care poate fi spălată maşina i (i=1,..,n). Să se determine ordinea de spălare a celor n maşini astfel încât timpul de staţionare al unei maşini în staţie să fie minim.

5. Metoda Divide et Impera

5- Problema turnurilor din Hanoi. Se dau trei tije A, B, C, pe tija A aflându-se n discuri de dimensiuni diferite, aranjate de la bază spre vârf de la cel mai mare la cel mai mic. Ştiind că se mută câte un disc la un moment dat şi că nu se poate muta un disc mai mare peste un disc mai mic, să se mute toate cele n discuri de pe tija A pe tija B utilizând drept ajutor tija C. Scrieţi un program care să afişeze mutările necesare deplasării.

5- Se dă o bucată dreptunghiulară de tablă cu lungimea l şi înălţimea h, având pe suprafaţa ei n găuri de coordonate numere întregi. Se cere să se decupeze din ea o bucată de arie maximă care nu prezintă găuri. Sunt permise numai tăieturi verticale şi orizontale.

5- Fiind dat un şir de numere naturale a₁, a₂,...,a_n, determinaţi lungimea celei mai lungi subsecvenţe crescătoare. O subsecvenţă crescătoare este o listă cu , unde m este lungimea subsecvenţei. Scrieţi un algoritm pentru a determina cea mai lungă subsecvenţă crescătoare utilizând metoda Divide-et-Impera (O(n²)).

5- Realizaţi un algoritm pentru înmulţirea a n numere complexe utilizând numai 3(n-1) înmulţiri de numere reale, folosind metoda Divide-et-Impera.

5- Fiind dat un şir de numere naturale a₁, a₂, ..., a_n () se cere determinarea numărului de perechi (i, j) cu proprietatea i<j şi a_i>a_j.

Observaţie: În cazul unui număr mai mare de date este bine ca acestea să fie citite dintr-un fişier text.

5- Se consideră un şir de elemente numere întregi. Să se verifice dacă un număr aparţine şirului utilizând căutarea binară.

5- Se consideră un vector de lungime n. Definim plierea vectorului prin suprapunerea unei jumătăţi numită donatoare peste cealaltă jumătate numită receptoare cu precizarea că dacă numărul de elemente este impar, elementul din mijloc este eliminat. În acest mod se ajunge la un subşir ale cărui elemente au numerotarea corespunzătoare jumătăţii receptoare.

Exemplu: vectorul (1, 2, 3, 4, 5) se poate plia în două moduri (1, 2) sau (4, 5), elementul 3 fiind eliminat conform ipotezei. Plierea se poate aplica în continuare în mod repetat până când se ajunge la un subşir de lungime 1, numit element final.

1. Fiind dat să se determine dacă elementul i poate fi element final ca rezultat al unor plieri succesive.
2. Să se precizeze toate elementele finale posibile.
3. Fiind dat un element i final, să se afişeze o succesiune de plieri prin care se ajunge la el.
4. Considerăm că valorile vectorului sunt numere întregi citite de la tastatură. Prin pliere din dublul valorii fiecărui element al jumătăţii receptoare se scade valoarea elementului corespunzător jumătăţii donatoare.
5. Să se verifice dacă există un element final cu valoarea 0 după ultima pliere şi, în caz afirmativ să se determine succesiunea de plieri corespunzătoare.

6. Metoda Backtracking

6- Să se genereze permutări de n elemente.

6- Să se genereze combinări de n luate câte k.

6- Să se genereze aranjamente de n luate câte k.

6- Să se parcurgă cu un cal o tablă de şah trecând o singură dată prin toate căsuţele.

6- Fiind dată o hartă cu n ţări, se cer toate soluţiile de colorare a acesteia, astfel încât două ţări cu frontiera comună să fie colorate diferit. Se ştie faptul că sunt suficiente numai 4 culori pentru ca orice hartă să poată fi colorată.

6- Se dă o sumă s şi n tipuri de monede având valori lei. Se cere modalitatea de plată a sumei s utilizând un număr minim de monede.

6- Se dă o sumă s şi n tipuri de monede având valori lei din fiecare tip putând dispune de numai monede. Se cere modalitatea de plată minimală (din punct de vedere al numărului de monede) a sumei s utilizând aceste monede.

6- Orice număr natural se poate scrie ca o sumă de termeni, fiecare termen fiind un număr natural diferit de zero.

Exemplu: 4=3+1=2+2=2+1+1=1+1+1+1.

Notăm cu T(n) numărul de modalităţi distincte în care se poate scrie n ca sumă de numere naturale strict pozitive. Pentru n=4, T(n)=4. Realizaţi un program care să calculeze pentru un n dat () pe T(n).

6- Un grup de n persoane sunt aşezate pe un rând de scaune. Între oricare doi vecini izbucnesc conflicte de interese astfel încât aceştia se reaşează în rând dar între oricare doi foşti vecini trebuie să existe una sau cel mult două persoane. Să se realizeze un program care să afişeze toate variantele de reaşezare posibile.

6- Se dă un număr natural par n. Să se determine toate şirurile de n paranteze care se închid corect.

Exemplu: n=6 ((())), (()()), ()()(), ()(()), (())().

6- Dintr-un grup de n persoane, dintre care p femei, trebuie formată o delegaţie de k persoane, din care m femei. Să se precizeze toate delegaţiile care se pot forma.

6- Se dau n persoane şi acelaşi număr de apartamente. Fiecare persoană îşi indică opţiunea pentru fiecare apartament. Se cere să se repartizeze apartamentele astfel încât gradul de satisfacere a dorinţelor să fie maxim. Cu cât un apartament este mai dorit preferinţa pentru el are o valoare mai mică, deci gradul maxim de satisfacere se va obţine prin minimizarea sumei preferinţelor fiecărei persoane faţă de apartamentul ce-i va fi repartizat.

6- Pe un mal se află n perechi soţ-soţie. Ei trebuie să traverseze un râu având la dispoziţie o barcă de 2 locuri. Ştiind că barca nu merge singură şi nu trebuie să ramână un barbat singur cu soţia altuia, să se afişeze toate posibilităţile de trecere a râului.

6- Configuraţia unui teren este specificată printr-un caroiaj gen tablă de şah de dimensiune n, fiecare careu având o anumită cotă (înălţime). Într-un careu precizat al terenului se plasează o minge. Ştiind că mingea se poate deplasa într-unul din cele maximum 8 careuri vecine dacă acesta are o cotă strict mai mică, să se genereze toate traseele pe care le poate urma mingea pentru a părăsi terenul.

6- Se dă o matrice pătratică de dimensiuni nxn. Să se găsească drumul de cost minim de parcurgere a matricii din colţul din stânga-sus pâna în colţul din dreapta-jos. Costul unui drum este egal cu suma elementelor casuţelor prin care a trecut. Deplasarea se poate face numai pe verticală sau pe orizontală.

6- Să se scrie un program recursiv pentru a determina toate modalităţile de descompunere a unui număr în sumă de k numere naturale strict pozitive.

6- Se dă un caroiaj de dimensiune nxn. Se dau înălţimile fiecărei căsuţe. Să se găsească toate posibilităţile de a ieşi din caroiaj ştiind că persoana respectivă nu poate urca mai mult de h₀ şi coborâ mai mult de h₁.

6- O fotografie alb-negru este prezentată sub forma unei matrice binare. Ea înfăţişează unul sau mai multe obiecte. Porţiunile corespunzătoare unui obiect au valoarea 1. Se cere să se determine dacă fotografia reprezinta unul sau mai multe obiecte. Două puncte fac parte din acelaşi obiect dacă ele sunt vecine pe verticală, orizontală sau pe diagonală.

6- Se dă o matrice binară. Valorile 1 delimitează o suprafaţă închisă în cadrul matricei (elementele aparţinând acestei suprafeţe sunt marcate cu 0). Se dau, de asemenea, coordonatele x şi y ale unui punct din matrice. Să se coloreze suprafaţa din care face parte punctul respectiv.

6- Trebuie să deschidem seiful unei bănci. Acesta este protejat de o încuietoare cu cifru formată din n rotiţe. Fiecare rotiţă are pe ea inscripţionate cifre de la 0 la m-1. Un cod este format din secvenţa a n cifre, câte o cifră de pe fiecare rotiţă. Exsită o singură combinaţie care deschide seiful. Forma unui set de date este următoarea:

n m q cod₀ a₀ ... cod_q-1 a_q-1

unde este numărul de rotiţe, este numărul de cifre inscripţionate pe fiecare rotiţă, q>1 este numărul de încercări, cod_k este cea de-a k-a combinaţie încercată, iar reprezintă câte cifre din cod_k se potrivesc ca poziţie şi valoare cu cele din cifrul secret. Scrieţi un program care să determine cifrul secret pe baza încercărilor date.

6- Se consideră o tablă de şah de dimensiune nxn () pe care sunt dispuse obstacole. Se cere să se tipărească numărul minim de mutări necesare unui nebun pentru a se deplasa, respectând regulile jocului de şah şi ocolind obstacolele, dintr-o poziţie iniţială dată într-o poziţie finală dată. Datele se citesc în ordine:

• dimesiunea n a tablei de şah
• perechea (i,j) reprezentând poziţia iniţială a nebunului
• perechea (k,l) reprezentând poziţia finala a nebunului
• perechi de numere reprezentând poziţiile obstacolelor.

Se consideră că obstacolele nu coincid cu poziţia iniţială şi nici cu cea finală a nebunului.

7. Metoda programării dinamice

7- Se dă un şir de numere întregi. Să se determine cel mai lung subşir crescător al acestuia. Acest subşir nu trebuie format numai cu elemente situate pe poziţii consecutive în şirul iniţial.

7- O persoană dispune de n obiecte de greutăţi g₁, g₂, ..., g_n şi de un rucsac de capacitate maximă G. Câştigul pe care-l obţine persoana respectivă dacă transportă obiectul i este c_i. Să se determine obiectele care vor fi transportate în rucsac astfel încât câştigul să fie maxim. Obiectele sunt indivizibile: un obiect este fie luat în întregime fie nu este luat deloc.

Exemplu:

Avem la dispoziţie un rucsac de 15 kg. Ce obiecte ar trebui să luam astfel ca să maximizăm profitul (suma totală a valorilor obiectelor luate)? Care este valoarea maximă?

7- Se dă o mulţime de n numere întregi şi un număr M. Să se determine o submulţime a sa cu proprietatea că suma elementelor este egală cu M (dacă există!).

7- Se dau două şiruri de caractere A şi B. Să se determine cel mai lung subşir comun al celor două şiruri.

7- Se dau două şiruri de caractere A şi B cu n respectiv m caractere. Să se transforme cuvântul A în cuvântul B utilizând următoarele operaţii:

1. adăugarea unei litere - cost c₁
2. modificarea unei litere - cost c₂
3. ştergerea unei litere - cost c₃

Se defineşte costul unei transformări ca fiind suma costurilor tuturor operaţiilor efectuate. Se cere determinarea costului minim al transformării cuvântului A în cuvântul B precum şi a operaţiilor efectuate.

7- Pentru a putea înmulţi două matrici A şi B trebuie ca numărul de coloane al primei matrici A să fie egal cu numărul de linii al celei de-a doua matrici B. Pentru calculul matricei produs C=A*B, se vor realiza un număr de n*m*p înmulţiri. De exemplu dacă pentru calculul matricii C vor fi necesare 10x15x20 = 3000 de înmulţiri.

Pentru a înmulţi mai mult de două matrici putem să alegem ordinea în care facem înmulţirile matricilor. De exemplu pentru putem face produsul fie în aşa (XY)Z, fie aşa X(YZ). În primul mod vom avea 5*20*10 = 1000 înmulţiri pentru XY şi 5*35*20 = 3500 pentru rezultatul final, adică un total de 4500 înmulţiri. În cel de-al doilea mod vom avea 10*35*20 = 7000 înmulţiri pentru YZ şi 5*35*10 = 1750 pentru rezultatul final, adică un total de 8750 înmulţiri.

Fiind date dimensiunile unei secvenţe de matrici, trebuie determinată ordinea de înmulţire a acestora astfel încât numărul total de înmulţiri să fie minim.

Datele de intrare au următorul format: la început se citeşte n (numărul de matrici) urmat pe următoarele n linii de dimensiunile fiecărei matrici.

Exemplu:

Intrare:

Ieşire:

((A1 x (A2 x A3)) x ((A4 x A5) x A6))

7- Se dă un şir de n numere întregi (pozitive şi negative). Să se determine subşirul de numere situate pe poziţii consecutive care are suma maximă.

7- Se dă un şir de n numere întregi (conţin şi valori nule). Să se determine subşirul de numere situate pe poziţii consecutive ce are produsul maxim.

7- Se dă un dreptunghi ale cărui dimensiuni sunt numere naturale. Dreptunghiul trebuie decupat (descompus) în pătrate ale căror laturi sunt tot numere naturale şi sunt paralele cu laturile dreptunghiului iniţial. O tăietură într-un dreptunghi este obligatoriu făcută paralel cu o latură pe toată lungimea acesteia.

Se cere numărul minim de pătrate în care poate fi descompus dreptunghiul iniţial, respectâând regula de mai sus de efectuare a unei tăieturi într-un dreptunghi.

Lungimea şi lăţimea dreptunghiului nu vor depăşi 100.

Exemplu:

5 6

răspunsul este 3.

7- Avem un teren de formă pătrată împărţit în nxn parcele. Pe unele din aceste parcele se află amplasaţi copaci. Să se determine cea mai mare magazie de formă pătrată care poate fi amplasată pe teren fără să fie nevoie ca unii copaci să fie tăiaţi. Laturile magaziei trebuie să fie paralele cu axa orizontală, respectiv cea verticală. Datele de intrare constau din: numărul de parcele de pe o latură n (), numărul parcelelor pe care se află copaci t (), şi pe următoarele t linii câte două numere întregi indicând linia şi coloana unei parcele ce are pe suprafaţa ei copaci.

7- Se consideră un triunghi de numere naturale format din n linii. Prima linie conţine un număr, a doua linie două numere,... ultima linie n numere naturale. Cu ajutorul acestui triunghi se pot forma sume de numere naturale în felul următor:

- se porneşte cu numărul din linia 1.

- succesorul unui număr se afla pe linia următoare plasat sub el (aceeaşi coloană) sau pe diagonală, la dreapta (col+1).

Care este cea mai mare sumă care se poate forma astfel şi care sunt numerele care o alcătuiesc.

Exemplu.

2

3 5

6 3 4

5 6 1 4

7- Se consideră n camere distincte, situate una după alta, astfel încât din camera i () se poate trece doar în camera i+1. În fiecare cameră se găsesc mere, pere în cantităţi cunoscute.

O persoană cu un rucsac suficient de încăpător, iniţial gol, porneşte din camera 1, trece prin camerele 2,3,..,n şi iese. La intrarea în fiecare cameră descarcă rucsacul, şi încarcă fie toate merele, fie toate perele din camera respectivă, după care trece în camera următoare. Se presupune că pentru fiecare fruct transportat între două camere, persoana consumă o calorie. Ce fel de fructe trebuie să încarce persoana în rucsac astfel încât după parcurgerea celor n camere să consume un număr minim de calorii şi care este acest număr?

7- Se consideră n cuvinte de lungimi l₁,..., l_n (prin lungimea unui cuvânt înţelegem numărul de caractere din care este format cuvântul respectiv). Acestea trebuiesc aşezate în ordine într-un paragraf (un text format din mai multe linii) în care lungimea unei linii este l. Fiecare linie din paragraf începe cu un cuvânt. Se cunoaşte o distanţa optimă b (număr de spaţii prin care se separă două cuvinte), însă nu este obligatoriu ca aceasta să fie respectată (poate fi mai mică sau mai mare). Totuşi, distanţa dintre două cuvinte nu poate fi mai mică decât o valoare . Toate cuvintele au lungimi mai mici sau egale cu l. Pentru fiecare linie din paragraf se calculeaza un cost care însumează abaterile de la distanţa optimă între cuvinte la care se adauga spaţiile rămase libere după ultimul cuvânt din linie până la sfârşitul liniei. În cazul în care ultima linie este incompletă, costul ei este 0. Se defineşte costul paragrafării ca fiind suma costurilor liniilor care formează textul. Cum trebuie plasate cuvintele pe linii în aşa fel încât costul paragrafării să fie minim şi care este acesta?

7- Pe suprafaţa planetei Marte se adună mostre de rocă cu ajutorul unor vehicule speciale. Aceste vehicule se deplasează conform unei scheme de caroiaj doar spre sud sau est şi doar pe un teren lipsit de stânci. Harta pusă la dispoziţie conţine informaţii cu privire la poziţiile unde se află roci (o singură rocă se află într-o poziţie) şi unde sunt stânci. Harta este dată sub forma unei matrici de dimensiune nxm ce conţine elemente egale cu 0, 1, 2, având semnificaţia:

• 0 înseamnă teren gol
• 1 înseamnă rocă
• 2 înseamnă stâncă

Vehiculele pornesc din poziţia (1,1) reprezentând colţul din stânga sus al hărţii. Locul unde trebuie să ajungă vehiculele este colţul din dreapta jos al hărţii.

Să se scrie un program care determină numărul maxim de roci ce se pot aduna de un vehicul în drumul său.

Exemplu: